Benda putar

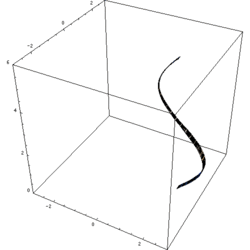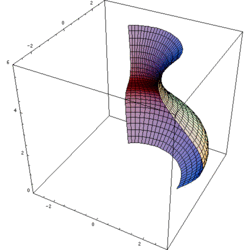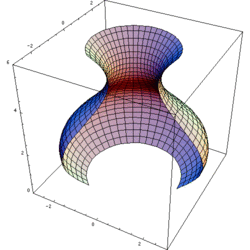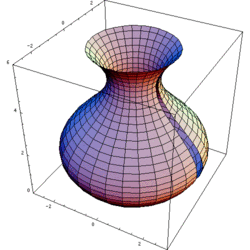
Dalam matematika, teknik, dan manufaktur, sebuah benda putar adalah sebuah gambar benda diperoleh dengan memutar sebuah kurva bidang sepanjang garis lurus (sumbu edar) yang terletak pada bidang yang sama.

Mengasumsi bahwa kurvanya tidak melintasi sumbu tersebut, volume benda sama dengan panjang dari lingkaran digambarkan oleh sentroid gambar yang dikalikan oleh luas gambar (teorema sentroid kedua Pappus).

Sebuah cakram wakilan adalah sebuah unsur volume sebuah benda putar. Unsur tersebut diciptakan dengan memutar sebuah ruas garis (panjang ${\displaystyle w}$) di sekitar sumbu tertentu (terletak ${\displaystyle r}$ satuan), jadi bahwa sebuah volume silindris ${\displaystyle \pi r^{2}w}$ satuan adalah tertutup.

Dua metode utama untuk mencari volume benda putar adalah metode integrasi cakram dan metode integrasi kulit. Untuk menerapkan metode-metode ini, ini adalah yang paling mudah untuk menggambar grafik dalam pertanyaan, mengenali luas yang akan diputar mengenai sumbu putar, menentukan volume dari salah satu sebuah irisan berbentuk cakram benda, dengan ketebalan ${\displaystyle \delta x}$, atau sebuah kulit silindris dengan lebar ${\displaystyle \delta x}$, dan kemudian cari jumlah limit volume-volume ini saat ${\displaystyle \delta x}$ mendekati 0, sebuah nilai yang dapat ditemukan dengan mengevaluasi sebuah integral yang sesuai. Sebuah pembenaran yang lebih teliti dapat diberikan dengan mencoba untuk mengevaluasi sebuah integral rangkap-tiga dalam koordinat silindris dengan dua urutan integrasi yang berbeda.

Metode cakram digunakan ketika irisannya yang digambar tegak lurus dengan sumbu edar; yaitu ketika mengintegralkan yang sejajar dengan sumbu edar.

Volume dari benda dibentuk dengan memutar luasnya diantara kurva ${\displaystyle f(x)}$ dan ${\displaystyle g(x)}$ dan garisnya ${\displaystyle x=a}$ dan ${\displaystyle x=b}$ mengenai sumbu-${\displaystyle x}$ diberikan dengan

$${\displaystyle V=\pi \int _{a}^{b}\left[f(x)^{2}-g(x)^{2}\right]\mathrm {d} x}$$

Jika ${\displaystyle g(x)=0}$ (misalnya memutar sebuah luas diantara kurva dan sumbu-${\displaystyle x}$), ini dikurangi menjadi

$${\displaystyle V=\pi \int _{a}^{b}f(x)^{2}\,\mathrm {d} x}$$

Metode tersebut dapat divisualkan dengan menganggap sebuah persegi panjang horizontal tipis pada ${\displaystyle y}$ diantara ${\displaystyle f(y)}$ di atas dan ${\displaystyle g(y)}$ di bawah, dan memutarnya mengenai sumbu-${\displaystyle y}$; ini membenetuk sebuah cincin (atau cakram dalam kasus bahwa ${\displaystyle g(y)=0}$, dengan jari-jari luar ${\displaystyle f(y)}$ dan jari-jari dalam ${\displaystyle g(y)}$. Luas sebuah cincin adalah ${\displaystyle \pi (R^{2}-r^{2})}$, dimana ${\displaystyle R}$ adalah jari-jari luar (pada kasus ${\displaystyle f(y)}$ ini), dan ${\displaystyle r}$ adalah jari-jari dalam (pada kasus ${\displaystyle g(y)}$ ini). Karena itu volume setiap cakram infinitesimal adalah ${\displaystyle \pi f(y)^{2}\,\mathrm {d} y}$. Limit jumlah Riemann dari volume cakram diantara ${\displaystyle a}$ dan ${\displaystyle b}$ menjadi integral (1).

Mengasumsi penerapan teorema Fubini dan mulitpeubah mengubah rumus variabel, metode cakram dapat diturunkan dengan cara yang lugas dengan (melambangkan benda sebagai ${\displaystyle D}$).

$${\displaystyle V=\iiint _{D}\mathrm {d} V=\int _{a}^{b}\int _{g(z)}^{f(z)}\int _{0}^{2\pi }r\,\mathrm {d} \theta \,\mathrm {d} r\,\mathrm {d} z=2\pi \int _{a}^{b}\int _{g(z)}^{f(z)}r\,\mathrm {d} r\,\mathrm {d} z=2\pi \int _{a}^{b}{\frac {1}{2}}r^{2}\Vert _{f(z)}^{g(z)}\,\mathrm {d} z=\pi \int _{a}^{b}f(z)^{2}-g(z)^{2}\,\mathrm {d} z}$$

Metode silinder digunakan ketika irisannya yang digambar sejajar dengan sumbu edar; yaitu ketika mengintegralkan yang tegak lurus dengan sumbu edar.

Volume dari benda dibentuk dengan memutar luasnya diantara kurva ${\displaystyle f(x)}$ dan ${\displaystyle g(x)}$ dan garisnya ${\displaystyle x=a}$ dan ${\displaystyle x=b}$ mengenai sumbu-${\displaystyle x}$ diberikan dengan

$${\displaystyle V=2\pi \int _{a}^{b}x|f(x)-g(x)|\,\mathrm {d} x}$$

Jika ${\displaystyle g(x)=0}$ (misalnya memutar sebuah luas diantara kurva dan sumbu-${\displaystyle y}$), ini dikurangi menjadi

$${\displaystyle V=2\pi \int _{a}^{b}x|f(x)|\,\mathrm {d} x}$$

Metode ini dapat divisualkan dengan menganggap sebuah persegi panjang vertikal yang tipis pada ${\displaystyle x}$ dengan tinggi ${\displaystyle f(x)-g(x)}$, dan memutarnya mengenai sumbu-${\displaystyle y}$; ini membentuk sebuah kulit silindris. Luas permukaan sisi silinder adalah ${\displaystyle 2\pi rh}$, dimana ${\displaystyle r}$ adalah jari-jari (pada kasus ${\displaystyle x}$ ini), dan ${\displaystyle h}$ adalah tinggi (pada kasus ${\displaystyle f(x)-g(x)}$ ini). Menjumlahkan semua dari luas permukaan sepanjang interval memberikan jumlah keseluruhan volume..

Metode ini dapat diturunkan dengan integral rangkap-tiga yang sama, kali ini dengan sebuah urutan integrasi yang berbeda.

$${\displaystyle V=\iiint _{D}\mathrm {d} V=\int _{a}^{b}\int _{g(r)}^{f(r)}\int _{0}^{2\pi }r\,\mathrm {d} \theta \,\mathrm {d} z\,\mathrm {d} r=2\pi \int _{a}^{b}\int _{g(r)}^{f(r)}r\,\mathrm {d} z\,\mathrm {d} r=2\pi \int _{a}^{b}r(f(r)-g(r))\,\mathrm {d} r}$$

Penampilan benda putar

Bentuk-bentuk yang tak bergerak

Bentuk-bentuknya yang bergerak, menunjukkan benda putar dibentuk oleh masing-masing

Ketika sebuah kurva didefinisikan oleh bentuk parametriknya ${\displaystyle (x(t),y(t))}$ dalam suatu interval ${\displaystyle [a,b]}$, volume dari benda dihasilkan dengan memutar kurva di sekitar sumbu-${\displaystyle x}$ dan sumbu-${\displaystyle y}$ diberikan dengan^[1]

$${\displaystyle V_{x}=\int _{a}^{b}\pi y^{2}\,{\frac {dx}{dt}}\,\mathrm {d} t{\text{ dan }}V_{y}=\int _{a}^{b}\pi x^{2}\,{\frac {dy}{dt}}\,\mathrm {d} t}$$

Dalam keadaan yang sama, luas dari permukaan benda dihasilkan dengan memutar kurva di sekitar sumbu-${\displaystyle x}$ dan sumbu-${\displaystyle y}$ diberikan dengan^[2]

$${\displaystyle A_{x}=\int _{a}^{b}2\pi y\,{\sqrt {\left({\frac {\mathrm {d} x}{\mathrm {d} t}}\right)^{2}+\left({\frac {\mathrm {d} y}{\mathrm {d} t}}\right)^{2}}}\,\mathrm {d} t{\text{ dan }}A_{y}=\int _{a}^{b}2\pi x\,{\sqrt {\left({\frac {\mathrm {d} x}{\mathrm {d} t}}\right)^{2}+\left({\frac {\mathrm {d} y}{\mathrm {d} t}}\right)^{2}}}\,\mathrm {d} t}$$

• Bola semu
• Integrasi cakram
• Integrasi kulit
• Permukaan putar
• Terompet Gabriel
• Teorema Guldinus
• Ungula

1. ^ Sharma, A. K. (2005). Application Of Integral Calculus. Discovery Publishing House. hlm. 168. ISBN 81-7141-967-4.
2. ^ Singh, Ravish R. (1993). Engineering Mathematics (Edisi 6th). Tata McGraw-Hill. hlm. 6.90. ISBN 0-07-014615-2.

• "Volumes of Solids of Revolution". CliffsNotes.com. 12 Apr 2011. Diarsipkan dari asli tanggal 2012-03-19.
• Ayres, Frank; Mendelson, Elliott (2008). Calculus. Schaum's Outlines. McGraw-Hill Professional. hlm. 244–248. ISBN 978-0-07-150861-2. (online copy, hlm. 244), pada Google Books
• (Inggris) Weisstein, Eric W. "Solid of Revolution". MathWorld.