Persamaan Fresnel
Persamaan Fresnel adalah deduksi matematis oleh Augustin Jean Fresnel hasil pengamatan perilaku gelombang cahaya ketika merambat antara medium yang mempunyai indeks bias yang berbeda. Persamaan Fresnel berlaku hanya pada indeks bias yang bernilai real, yaitu pada medium yang tidak menyerap gelombang cahaya. Indeks bias dapat mempunyai nilai imajiner dan bernilai kompleks, seperti pada medium logam atau semikonduktor yang menyerap gelombang cahaya. Persamaan ini juga berlaku hanya pada medium yang bersifat non magnetik dengan asumsi tidak terjadi interferensi.
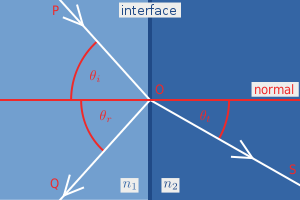
Saat gelombang cahaya merambat dari medium dengan indeks bias n1 ke medium dengan indeks bias n2, Fresnel berpendapat bahwa gelombang cahaya mengalami refleksi dan refraksi bersamaan. Pendapat ini berbeda dengan hukum Snellius yang menjelaskan bahwa partikel cahaya hanya membias pada kondisi yang sama.
Intensitas fraksi gelombang cahaya yang mengalami refleksi dari antarmuka ditentukan oleh reflektansi R dan fraksi gelombang cahaya yang mengalami refraksi ditentukan oleh transmitansi T.[1]
Perhitungan R bergantung pada polarisasi sinar insiden, disebut Refleksi Fresnel. Jika gelombang cahaya dipolarisasi oleh medan listrik yang tegak lurus bidang diagram (polarisasi-s), koefisien refleksi persamaan Fresnel menjadi:
dimana ?t dapat diturunkan dari ?i dengan hukum Snellius dan disederhanakan menggunakan identitas trigonometrik. Koefisien refleksi untuk polarisasi medan listrik pada bidang diagram (polarisasi-p) menjadi:
Koefisien transmisi untuk tiap-tiap bidang polarisasi dapat dihitung dengan aritmetika: Ts = 1 − Rs dan Tp = 1 − Rp.[2]
Jika sinar insiden tidak terpolarisasi (mempunyai nilai polarisasi-s dan -p), koefisien refleksi menjadi R = (Rs + Rp)/2.
Persamaan Fresnell untuk koefisien refleksi dengan koefisien amplitudo medan listrik menjadi:[3]
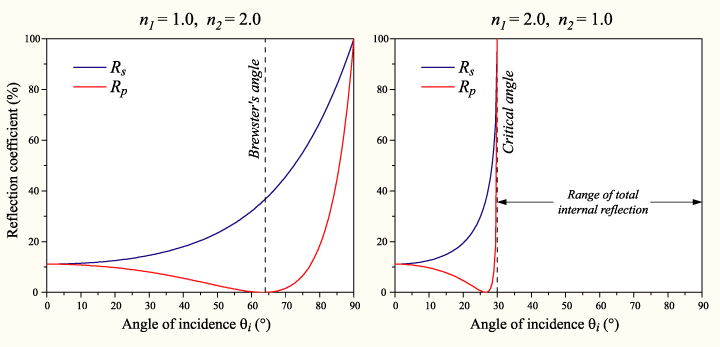
Pada sudut insiden tertentu, Rp bernilai nol. Hal ini menandakan refleksi keseluruhan dari gelombang cahaya pada bidang p. Sudut ini dikenal sebagai sudut Brewster, sekitar 56° untuk medium kaca dan udara.
Ketika gelombang cahaya merambat ke medium yang lebih renggang, n1 > n2, pada sudut insiden di atas sudut kritis semua gelombang cahaya mengalami refleksi dan Rs = Rp = 1. Fenomena ini disebut total internal reflection. Sudut kritis untuk kaca dan udara sekitar 41°.
Koefisien refleksi dan koefisien transmisi pada sudut insiden mendekati normal antarmuka (θi ≈ θt ≈ 0) dapat dihitung dengan persamaan:


![{\displaystyle R_{s}=\left[{\frac {\sin(\theta _{t}-\theta _{i})}{\sin(\theta _{t}+\theta _{i})}}\right]^{2}=\left({\frac {n_{1}\cos \theta _{i}-n_{2}\cos \theta _{t}}{n_{1}\cos \theta _{i}+n_{2}\cos \theta _{t}}}\right)^{2}=\left[{\frac {n_{1}\cos \theta _{i}-n_{2}{\sqrt {1-\left({\frac {n_{1}}{n_{2}}}\sin \theta _{i}\right)^{2}}}}{n_{1}\cos \theta _{i}+n_{2}{\sqrt {1-\left({\frac {n_{1}}{n_{2}}}\sin \theta _{i}\right)^{2}}}}}\right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b92746c5ddf76cd0560b4798438aa7efc04f009)
![{\displaystyle R_{p}=\left[{\frac {\tan(\theta _{t}-\theta _{i})}{\tan(\theta _{t}+\theta _{i})}}\right]^{2}=\left({\frac {n_{1}\cos \theta _{t}-n_{2}\cos \theta _{i}}{n_{1}\cos \theta _{t}+n_{2}\cos \theta _{i}}}\right)^{2}=\left[{\frac {n_{1}{\sqrt {1-\left({\frac {n_{1}}{n_{2}}}\sin \theta _{i}\right)^{2}}}-n_{2}\cos \theta _{i}}{n_{1}{\sqrt {1-\left({\frac {n_{1}}{n_{2}}}\sin \theta _{i}\right)^{2}}}+n_{2}\cos \theta _{i}}}\right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/269fc0d8deb5f59f0349c28ad15504fc8ed44aff)