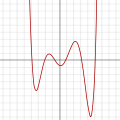Polinomial

Dalam matematika, polinomial atau suku banyak (juga ditulis sukubanyak) adalah pernyataan matematika yang melibatkan jumlahan perkalian pangkat dalam satu atau lebih variabel dengan koefisien. Secara umum, sebuah polinomial satu variabel memiliki bentuk seperti berikut:
dengan merupakan bilangan cacah, dan dengan merupakan koefisien konstan.
Pangkat tertinggi pada suatu polinomial menunjukkan orde atau derajat dari polinomial tersebut.
Operasi
Penjumlahan dan pengurangan
Perkalilan
Pembagian dan pemfaktoran
Grafik polinomial
Graphs
-
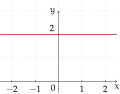
Polinomial berderajat 0: f(x) = 2
-
Polinomial berderajat 1: f(x) = 2x + 1
-
Polinomial berderajat 2: f(x) = x2 − x − 2 = (x + 1)(x − 2)
-
Polinomial berderajat 3: f(x) = x3/4 + 3x2/4 − 3x/2 − 2 = 1/4 (x + 4)(x + 1)(x − 2)
-
Polinomial berderajat 4: f(x) = 1/14 (x + 4)(x + 1)(x − 1)(x − 3)
+ 0.5 -
Polinomial berderajat 5: f(x) = 1/20 (x + 4)(x + 2)(x + 1)(x − 1)
(x − 3) + 2 -
Polinomial berderajat 6: f(x) = 1/100 (x6 − 2x 5 − 26x4 + 28x3 + 145x2 − 26x − 80)
-
Polinomial berderajat 7: f(x) = (x − 3)(x − 2)(x − 1)(x)(x + 1)(x + 2) (x + 3)
Fungsi polinomial satu variabel dapat ditampilkan dalam bentuk grafik.
- Grafik dari polinomial noladalah sumbu-.
- Grafik dari polinomial berderajat nol (disebut juga fungsi konstan)adalah garis mendatar yang berpotongan di titik (0,a0)
- Grafik dari polinomial berderajat satu (disebut juga fungsi linear)adalah berupa garis miring dengan y memotong di a0 dengan kemiringan sebesar a1.
- Grafik dari polinomial berderajat dua (disebut juga fungsi kuadrat)merupakan parabola.
- Grafik dari polinomial berderajat tigamerupakan kurva pangkat 3.
- Grafik dari polinomial berderajat dua atau lebihmerupakan kurva kontinu tak lurus.
Polinomial dan kalkulus
Untuk menghitung turunan dan integral dari polinomial tidaklah terlalu sulit. Untuk fungsi polinomial
maka turunan terhadap x adalah
dan integral tak tentu terhadap x adalah
Bacaan lebih lanjut
- Kurnianingsih, Sri (2007). Matematika SMA dan MA 2B Untuk Kelas XI Semester 2 Program IPA. Jakarta: Esis/Erlangga. ISBN 979-734-503-3. (Indonesia)
- Abdillah Ahmad, dkk (2023). Kawan Tanding Olimpiade Matematika - A. Bandung: Tim KTO Matematika
Pranala luar
Wikimedia Commons memiliki media mengenai Polynomials.
- (Inggris)Polinomial Artikel tentang polinomial di Wolfram MathWorld