Ruang vektor berdimensi hingga

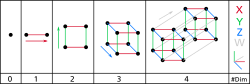
Pada matematika, dimensi pada ruang vektor V adalah kardinalitas (misalnya jumlah vektor) dari basis V terhadap basis lapangannya.^[1][2] Hal ini biasanya dikenal sebagai dimensi Hamel (berdasarkan Georg Hamel) atau dimensi aljabar untuk membedakannya dengan dimensi tipe lain.

Untuk setiap ruang vektor, terdapat sebuah basis,^[a] dan setiap basis dari ruang vektor memiliki kardinalitas yang setara.^[b] Maka, dimensi dari ruang vektor didefinisikan secara unik. Ruang vektor V dikatakan berdimensi hingga jika dimensi dari V bernilai hingga, dan dikatakan berdimensi takhingga jika dimensinya takhingga.

Dimensi dari ruang vektor V terhadap lapangan F dapat dituliskan sebagai dim_F(V) atau [V : F]. Ketika F dapat disimpulkan dari konteks, penulisan dimensi tersebut dapat disederhanakan menjadi dim(V).

Ruang vektor ${\displaystyle \mathbb {R} }$³ memiliki

$${\displaystyle \left\{{\begin{pmatrix}1\\0\\0\end{pmatrix}},{\begin{pmatrix}0\\1\\0\end{pmatrix}},{\begin{pmatrix}0\\0\\1\end{pmatrix}}\right\}}$$

sebagai basis standar, maka dim_{${\displaystyle \mathbb {R} }$}(${\displaystyle \mathbb {R} }$³) = 3. Lebih umum, dim_{${\displaystyle \mathbb {R} }$}(${\displaystyle \mathbb {R} }$ⁿ) = n; atau yang lebih umum dim_F(Fⁿ) = n untuk semua lapangan F.

Bilangan kompleks ${\displaystyle \mathbb {C} }$ bernilai riil dan kompleks pada ruang vektor; dengan dim_{${\displaystyle \mathbb {R} }$}(${\displaystyle \mathbb {C} }$) = 2 dan dim_{${\displaystyle \mathbb {C} }$}(${\displaystyle \mathbb {C} }$) = 1. Maka, dimensinya bergantng pada basis lapangan.

Hanya ruang vektor dengan dimensi 0 bernilai { 0 }, ruang vektor yang hanya berisi elemen nolnya.

• Axler, Sheldon (2015). Linear Algebra Done Right. Undergraduate Texts in Mathematics (Edisi 3). Springer. ISBN 978-3-319-11079-0. Pemeliharaan CS1: Ref menduplikasi bawaan (link)