Tesseract (geometri)
| Tesseract 8-cell Kubus empat dimensi | |
|---|---|
| Tipe | Politop dimensi empat beraturan konveks |
| Simbol Schläfli | {4,3,3} t0,3{4,3,2} atau {4,3}×{ } t0,2{4,2,4} atau {4}×{4} t0,2,3{4,2,2} atau {4}×{ }×{ } t0,1,2,3{2,2,2} atau { }×{ }×{ }×{ } |
| Sel | 8 {4,3} |
| Wajah | 24 {4} |
| Tepi | 32 |
| Grup Coxeter | B4, [3,3,4] |
| Dual | 16-cell |
| Properti | cembung, isogonal, isotoxal, isohedral |
| Indeks seragam | 10 |
Dalam geometri, tesseract adalah sebuah bangun ruang dimensi empat yang mirip dengan sebuah kubus, dalam artian bahwa tesseract menyerupai sebuah kubus yang menyerupai persegi. Mirip seperti permukaan kubus yang terdiri dari enam muka persegi, hiperpermukaan dari tesseract terdiri dari delapan sel kubus. Tesseract merupakan salah satu dari enam politop berdimensi empat beraturan cembung.
Tesseract juga disebut 8-cell (bahasa Indonesia: sel-8), C8, oktakoron (beraturan), oktahedroid,[1] prisma kubik, dan tetrakubus.[2] Tesseract merupakan hiperkubus dimensi empat, sebagai bagian dari keluarga berdimensi hiperkubus atau politop ukuran (bahasa Inggris: measure polytope).[3] Coxeter melabelinya sebagai politop .[4]
Menurut Oxford English Dictionary, kata tesseract berasal dari Charles Howard Hinton dalam bukunya 1888, yang berjudul A New Era of Thought. Kata tesseract diambil dari bahasa Yunani τέσσερεις (téssereis, yang berarti "empat") dan ἀκτίνες (aktines, yang berarti "sinar"), dan kata tersebut merujuk ke empat rusuk dari masing-masing titik sudut ke titik sudut lain.[5]
Geometri
Tesseract merupakan politop beraturan dengan tiga kubus yang dilipat di sekitar masing-masing rusuk, karena itu tesseract mempunyai simbol Schläfli {4,3,3} dengan simetri hiperoktahedral dari orde 384. Dibangun sebagai dalam hiperprisma dimensi empat yang terbuat dari dua kubus yang sejajar, tesseract dapat dinamai sebagai simbol Schläfli komposit {4,3} × { }, dengan orde simetri 96. Karena disebut sebagai duoprisma 4-4, sebuah darab Kartesius dari dua persegi, tesseract dapat dinamai dengan simbol Schläfli komposit {4}×{4}, dengan orde simetri 64. Karena berupa ortotop, tesseract dapat dinyatakan dengan simbol Schläfli komposit { } × { } × { } × { } atau { }4, dengan orde simetri 16.
Karena masing-masing titik sudut tesseract berdampingan dengan empat rusuk, bangunan puncak (bahasa Inggris: vertex figure) dari tesseract adalah sebuah tetrahedron beraturan. Politop dual dari tesseract disebut heksadekakoron beraturan atau 16-cell (bahasa Indonesia: sel-16), yang dinyatakan dengan simbol Schläfli {3,3,4} dan dapat digabungkan menjadi gabungan dari tesseract dan 16-cell.
Koordinat
Tesseract dalam bentuk standar dalam ruang empat dimensi Euklides dinyatakan sebagai lambung cembung dari titik (±1, ±1, ±1, ±1). Hal ini mengartikan bahwa tesseract merupakan bangunan yang terdiri dari titik:
Dalam kerangka acuan Cartesius, tesseract mempunyai radius 2 dan dibatasi dengan delapan hiperbidang (). Perpotongan dari masing-masing pasangan dari hiperbidang tak sejajar membentuk 24 muka persegi di sebuah tesseract. Tiga kubus dan tiga persegi memotong di masing-masing rusuk. Selain itu, terdapat empat kubus, enam persegi, dan empat rusuk yang bertemu di setiap titik sudut. Secara keseluruhan, tesseract mempunyai 8 kubus, 24 persegi, 32 rusuk, dan 16 titik sudut.
Konstruksi

Konstruksi hiperkubus dapat dibayangkan sebagai berikut:
- dimensi 1: Dua titik dan dapat dihubungkan menjadi sebuah garis, sehingga memberikan segmen garis baru .
- dimensi 2: Dua segmen garis sejajar dan dipisah dengan jarak . Kedua segmen garis tersebut dapat dihubungkan menjadi sebuah persegi, dengan sudut-sudutnya ditandai sebagai .
- dimensi 3: Dua persegi sejajar dan dipisah dengan jarak . Kedua persegi tersebut dapat dihubungkan menjadi sebuah kubus, dengan sudut-sudutnya ditandai sebagai .
- dimensi 4: Dua kubus sejajar dan dipisah dengan jarak . Kedua kubus tersebut dapat dihubungkan menjadi sebuah tesseract, dengan sudut-sudutnya ditandai sebagai . Akan tetapi, penyusunan yang sejajar dari kedua kubus membuat masing-masing dari kedelapan pasangan titik sudut dipisah dengan jarak . Hal ini dapat diperoleh dalam ruang dimensi 4 atau lebih.
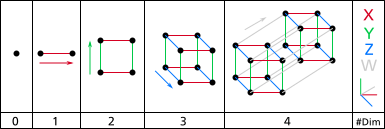
Rumus
Berikut adalah rumus-rumus untuk sebuah tesseract dengan panjang rusuk :
- Hipervolume:
- Volume permukaan:
- Diagonal muka:
- Diagonal sel:
- Diagonal ruang dimensi 4:
Sebagai konfigurasi
Matriks konfigurasi di bawah mewakili sebuah tesseract, dengan baris dan kolomnya menyatakan titik sudut, rusuk, muka, dan sel. Bilangan diagonal di matriks menunjukkan banyaknya masing-masing elemen yang muncul di seluruh tesseract, sedangkan bilangan non-diagonal menunjukkan banyaknya elemen di kolom yang muncul di dalam atau di elemen baris.[6]
Proyeksi
Tesseract dapat diproyeksi menjadi ruang dimensi dua dan tiga, sama halnya dengan kubus yang diproyeksi menjadi ruang dimensi dua.
- Proyeksi sejajar cell-first dari tesseract menjadi ruang dimensi tiga mempunyai sampul yang berbentuk kubus. Sel yang terdekat dan terjauh diproyeksi ke sebuah kubus, dan sedangkan enam sel yang tersisa diproyeksi ke enam muka persegi dari kubus.
- Proyeksi sejajar face-first dari tesseract menjadi ruang dimensi tiga mempunyai sampul berbentuk balok. Dua pasangan sel diproyeksi ke setengah batas atas dan batas bawah sampul tersebut, sedangkan empat sel yang tersisa diproyeksi ke muka sisi.
- Proyeksi sejajar edge-first dari tesseract menjadi ruang dimensi tiga mempunyai sebuah sampul berbentuk prisma heksagonal. Enam sel diproyeksi ke prisma berbentuk belah ketupat yang disusun dalam prisma heksagonal, sama halnya dengan muka dari kubik dimensi tiga diproyeksi ke enam belah ketupat dalam sampul heksagonal melalui proyeksi vertex-first. Dua sel lainnya diproyeksi ke alas prisma.
- Proyeksi sejajar vertex-first dari tesseract menjadi ruang dimensi tiga mempunyai sampul yang berbentuk dodekahedron belah ketupat. Dua titik sudut dari tesseract diproyeksi ke titik asal. Setidaknya ada dua cara memisahkan sebuah dodekahedron belah ketupat menjadi empat rombohedron yang kongruen, sehingga totalnya berjumlah delapan rhombohedron yang memproyeksi kubus dari tesseract. Proyeksi ini juga mempunyai volume maksimum, dengan himpunan dari vektor proyeksi adalah , , .
| Bidang Coxeter | B4 | B3 / D4 / A2 | B2 / D3 |
|---|---|---|---|
| Graf | 
|

|

|
| Simetri dihedral | [8] | [6] | [4] |
| Bidang Coxeter | Lain-lain | F4 | A3 |
| Graf | 
|

|

|
| Simetri dihedral | [2] | [12/3] | [4] |
Catatan
- ^ Matila Ghyka, The geometry of Art and Life (1977), hlm. 68
- ^ Istilah ini juga dapat diartikan sebagai polikubus (policube) yang terdiri dari empat kubus.
- ^ Elte, E. L. (1912). Polytopes Semiregular dari Hyperspaces. Groningen: University of Groningen. ISBN 1-4181-7968-X.
- ^ Coxeter 1973, hlm. 122-123, §7.2. illustration Fig 7.2C.
- ^ "tesseract". Oxford English Dictionary (Edisi Online). Oxford University Press. 199669. Templat:OEDsub
- ^ Coxeter 1973, hlm. 12, §1.8 Configurations.
Lihat pula
Referensi
- Coxeter, H.S.M. (1973). Polytopes biasa (Edisi 3rd). New York: Dover. hlm. 122–123.
- F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss (1995) Kaleidoscopes: Selected Writings of H.S.M. Coxeter, Wiley-Interscience Publication ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, Mathematische Zeitschrift 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1n1)
- T. Gosset (1900) On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan.
- T. Proctor Hall (1893) "The projection of fourfold figures on a three-flat", American Journal of Mathematics 15:179–89.
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
- Victor Schlegel (1886) Ueber Projectionsmodelle der regelmässigen vier-dimensionalen Körper, Waren.
Pranala luar
- (Inggris) Weisstein, Eric W. "Tesseract". MathWorld.
- Klitzing, Richard. "4D uniform polytopes (polychora) x4o3o3o - tes".
- The Tesseract Ray traced images with hidden surface elimination. This site provides a good description of methods of visualizing 4D solids.
- Der 8-Zeller (8-cell) Marco Möller's Regular polytopes in ℝ4 (German)
- WikiChoron: Tesseract
- HyperSolids is an open source program for the Apple Macintosh (Mac OS X and higher) which generates the five regular solids of three-dimensional space and the six regular hypersolids of four-dimensional space.
- Hypercube 98 A Windows program that displays animated hypercubes, by Rudy Rucker
- ken perlin's home page A way to visualize hypercubes, by Ken Perlin
- Some Notes on the Fourth Dimension includes animated tutorials on several different aspects of the tesseract, by Davide P. Cervone
- Tesseract animation with hidden volume elimination





























