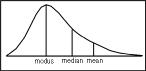
Ukuran pemusatan data

Ukuran pemusatan data adalah sembarang ukuran yang menunjukkan pusat segugus data, yang telah diurutkan dari yang terkecil sampai yang terbesar atau sebaliknya dari yang terbesar sampai yang terkecil.^[1] Salah satu kegunaan dari ukuran pemusatan data adalah untuk membandingkan dua (populasi) atau contoh, karena sangat sulit untuk membandingkan masing-masing anggota dari masing-masing anggota populasi atau masing-masing anggota data contoh.^[2] Nilai ukuran pemusatan ini dibuat sedemikian sehingga cukup mewakili seluruh nilai pada data yang bersangkutan.^[2]

Ukuran pemusatan yang paling banyak digunakan adalah median, mean, dan modus.^[1] Masing-masing dari ukuran pemusatan data tersebut memiliki kekurangan.^[1] Nilai tengah akan sangat dipengaruh nilai pencilan.^[1] Median terlalu bervariasi untuk dijadikan parameter populasi.^[1] Sedangkan modus hanya dapat diterapkan dalam data dengan ukuran yang besar.^[1]

• Mean

merupakan rata-rata hitung

$${\displaystyle {\bar {x}}={\frac {x_{1}+x_{2}+x_{3}+\cdots +x_{n}}{n}}=\sum \limits _{i=0}^{n}{\frac {x_{i}}{n}}}$$

• Median

merupakan nilai tengah setelah diurutkan

bila ganjil maka terambil di tengah setelah diurutkan. bila genap terambil dua di tengah dibagi rata-rata setelah diurutkan

${\displaystyle Me=x_{\frac {n+1}{2}}}$ bila n ganjil

${\displaystyle Me={\frac {x_{\frac {n}{2}}+x_{({\frac {n}{2}}+1)}}{2}}}$ bila n genap

• Modus

merupakan nilai yang paling sering muncul atau nilai yang mempunyai frekuensi tertinggi

terambil jumlahnya paling banyak setelah diurutkan

• Kuartil

merupakan membagi data menjadi empat bagian yang sama banyak

${\displaystyle Q_{i}={\frac {i(n+1)}{4}}}$

terdiri dari tiga jenis yaitu kuartil bawah, tengah dan atas.

Kuartil	Ganjil		Genap
	n+1 tidak habis dibagi 4	n+1 habis dibagi 4	n tidak habis dibagi 4	n habis dibagi 4
Kuartil bawah (Q1)	${\displaystyle {\frac {x_{\frac {n-1}{4}}+x_{({\frac {n-1}{4}}+1)}}{2}}}$	${\displaystyle x_{\frac {n+1}{4}}}$	${\displaystyle x_{\frac {n+2}{4}}}$	${\displaystyle {\frac {x_{\frac {n}{4}}+x_{({\frac {n}{4}}+1)}}{2}}}$
Kuartil tengah (Q2)	${\displaystyle x_{\frac {n+1}{2}}}$		${\displaystyle {\frac {x_{\frac {n}{2}}+x_{({\frac {n}{2}}+1)}}{2}}}$
Kuartil atas (Q3)	${\displaystyle {\frac {x_{\frac {3n+1}{4}}+x_{({\frac {3n+1}{4}}+1)}}{2}}}$	${\displaystyle x_{\frac {3(n+1)}{4}}}$	${\displaystyle x_{\frac {3n+2}{4}}}$	${\displaystyle {\frac {x_{\frac {3n}{4}}+x_{({\frac {3n}{4}}+1)}}{2}}}$

atau

Kuartil	Ganjil	Genap
Kuartil bawah (Q1)	${\displaystyle {\frac {n+1}{4}}}$	${\displaystyle {\frac {n+2}{4}}}$
Kuartil tengah (Q2)	${\displaystyle {\frac {n+1}{2}}}$	${\displaystyle {\frac {X_{{\frac {n}{2}}+X_{({\frac {n}{2}}+1)}}}{2}}}$
Kuartil atas (Q3)	${\displaystyle {\frac {3\cdot (n+1)}{4}}}$	${\displaystyle {\frac {3n+2}{4}}}$

• Desil

merupakan membagi data menjadi sepuluh bagian yang sama banyak

${\displaystyle D_{i}={\frac {i(n+1)}{10}}}$

terdiri dari tiga jenis yaitu desil bawah, tengah dan atas. untuk menentukan rumusnya sama dengan tabel yang dibuat data kuartil.

• Persentil

merupakan membagi data menjadi seratus bagian yang sama banyak

${\displaystyle P_{i}={\frac {i(n+1)}{100}}}$

terdiri dari tiga jenis yaitu presentil bawah, tengah dan atas. untuk menentukan rumusnya sama dengan tabel yang dibuat data kuartil.

Dalam data berkelompok terdiri dari tabel, diagram garis, diagram batang serta diagram lingkaran.

• Mean

${\displaystyle {\bar {x}}={\frac {f_{1}x_{1}+f_{2}x_{2}+f_{3}x_{3}+\cdots +f_{n}x_{n}}{f_{1}+f_{2}+f_{3}+\cdots +f_{n}}}={\frac {\sum \limits _{i=1}^{n}{f_{i}x_{i}}}{\sum \limits _{i=1}^{n}{f_{i}}}}}$

${\displaystyle {\bar {x}}={\bar {x_{s}}}+{\frac {\sum \limits _{i=1}^{n}{f_{i}d_{i}}}{\sum \limits _{i=1}^{n}{f_{i}}}}}$

${\displaystyle {\bar {x}}={\bar {x_{s}}}+({\frac {\sum \limits _{i=1}^{n}{f_{i}u}}{\sum \limits _{i=1}^{n}{f_{i}}}})c}$

keterangan

1. ${\displaystyle f_{i}}$ = frekuensi untuk nilai i
2. ${\displaystyle x_{i}}$ = data ke-i (untuk data tunggal) atau titik tengah rentang tertentu ke-i (data kelompok)
3. ${\displaystyle x_{s}}$= titik tengah rataan sementara
4. ${\displaystyle d_{i}}$ = panjang interval antar rentang tertentu pada ${\displaystyle x_{i}}$ (jika ${\displaystyle x_{s}}$ maka d adalah nol. Di atasnya bernilai min dan dibawahnya bernilai plus)
5. u = bilangan bulat (jika ${\displaystyle x_{s}}$ maka u adalah nol. diatasnya min serta dibawahnya plus)
6. c = panjang interval kelas

• Median

${\displaystyle Me=L_{2}+({\frac {{\frac {n}{2}}-(\sum {f})_{2}}{f_{Me}}})c}$

keterangan

1. ${\displaystyle L_{2}}$ = tepi bawah kelas median
2. n = banyak data
3. ${\displaystyle (\sum {f})_{2}}$ = jumlah frekuensi sebelum kelas median
4. ${\displaystyle f_{Me}}$ = frekuensi kelas median
5. c = panjang interval kelas

• Modus

${\displaystyle Mo=L_{o}+({\frac {d_{1}}{d_{1}+d_{2}}})c}$

keterangan

1. ${\displaystyle L_{o}}$ = tepi bawah kelas modus
2. ${\displaystyle d_{1}}$ = selisih frekuensi kelas modus dengan frekuensi kelas sebelum modus
3. ${\displaystyle d_{2}}$ = selisih frekuensi kelas modus dengan frekuensi kelas sesudah modus
4. c = panjang interval kelas

• Kuartil

${\displaystyle Q_{i}=L_{i}+({\frac {{\frac {in}{4}}-(\sum {f})_{i}}{f_{Q_{i}}}})c}$

keterangan

1. i = 1, 2 atau 3
2. ${\displaystyle L_{i}}$ = tepi bawah kelas kuartil ke-i
3. n = banyak data
4. ${\displaystyle (\sum {f})_{i}}$ = jumlah frekuensi sebelum kelas kuartil ke-i
5. ${\displaystyle f_{Q_{i}}}$ = frekuensi kelas kuartil ke-i
6. c = panjang interval kelas

• Desil

${\displaystyle D_{i}=L_{i}+({\frac {{\frac {in}{10}}-(\sum {f})_{i}}{f_{D_{i}}}})c}$

keterangan

1. i = 1, 2, 3, ....., 9
2. ${\displaystyle L_{i}}$ = tepi bawah kelas desil ke-i
3. n = banyak data
4. ${\displaystyle (\sum {f})_{i}}$ = jumlah frekuensi sebelum kelas desil ke-i
5. ${\displaystyle f_{Q_{i}}}$ = frekuensi kelas desil ke-i
6. c = panjang interval kelas

• Persentil

${\displaystyle P_{i}=L_{i}+({\frac {{\frac {in}{100}}-(\sum {f})_{i}}{f_{P_{i}}}})c}$

keterangan

1. i = 1, 2, 3, ....., 99
2. ${\displaystyle L_{i}}$ = tepi bawah kelas persentil ke-i
3. n = banyak data
4. ${\displaystyle (\sum {f})_{i}}$ = jumlah frekuensi sebelum kelas persentil ke-i
5. ${\displaystyle f_{Q_{i}}}$ = frekuensi kelas persentil ke-i
6. c = panjang interval kelas

• Lima serangkai

${\displaystyle x_{min}}$

${\displaystyle Q_{1}}$

${\displaystyle Q_{2}}$

${\displaystyle Q_{3}}$

${\displaystyle x_{max}}$

• Rataan dua

${\displaystyle R_{2}={\frac {Q_{1}+Q_{3}}{2}}}$

• Rataan tiga

${\displaystyle R_{3}={\frac {Q_{1}+2Q_{2}+Q_{3}}{2}}}$

• Jangkauan atau Range

${\displaystyle J=x_{max}-x_{min}}$

• Jangkauan kuartil atau Hamparan

${\displaystyle H=Q_{3}-Q_{1}}$

• Jangkauan semi kuartil atau Simpangan kuartil

${\displaystyle Q_{d}={\frac {Q_{3}-Q_{1}}{2}}}$

• Simpangan rata-rata

Data tunggal

${\displaystyle SR={\frac {\sum {|x_{i}-{\bar {x}}|}}{n}}}$

Data berkelompok

${\displaystyle SR={\frac {\sum \limits _{i=1}^{n}{f_{i}|x_{i}-{\bar {x}}|}}{\sum \limits _{i=1}^{n}{f_{i}}}}}$

• Ragam atau Varian

Data tunggal

${\displaystyle V={\frac {\sum {|x_{i}-{\bar {x}}|^{2}}}{n}}}$

Data berkelompok

${\displaystyle V={\frac {\sum \limits _{i=1}^{n}{f_{i}|x_{i}-{\bar {x}}|^{2}}}{\sum \limits _{i=1}^{n}{f_{i}}}}}$

• Simpangan baku atau deviasi

${\displaystyle SB={\sqrt {V}}}$

Data tunggal

${\displaystyle S={\sqrt {\frac {\sum {|x_{i}-{\bar {x}}|^{2}}}{n}}}}$

Data berkelompok

${\displaystyle S={\sqrt {\frac {\sum \limits _{i=1}^{n}{f_{i}|x_{i}-{\bar {x}}|^{2}}}{\sum \limits _{i=1}^{n}{f_{i}}}}}}$

• Ukuran penyebaran data
• Probabilitas
• Statistika matematika