Analisis riil

Analisis riil atau analisis real (bahasa Inggris: real analysis), atau biasanya disebut teori fungsi variabel riil atau teori fungsi peubah riil merupakan cabang dari analisis matematika yang membahas himpunan bilangan riil, fungsi riil, serta barisan dan deret bilangan riil.^[1] Singkatnya, analisis riil adalah cabang analisis matematis yang berkaitan dengan bilangan riil dan fungsi bernilai riil dari variabel riil.^[2][3] Analisis riil dapat dianggap sebagai kalkulus yang lebih mendalam, dan juga pembahasan secara lebih mendalam mengenai konsep barisan dan limit, kekontinuan, turunan, integral, dan barisan dari fungsi tersebut.

Penjelasan analisis riil pada buku-buku pelajaran tingkat lanjut biasanya dimulai dengan pembuktian sederhana mengenai teori dasar himpunan, pendefinisian konsep-konsep fungsi yang jelas, dan pengenalan kepada bilangan asli dan pentingnya teknik pembuktian menggunakan induksi matematika. Lalu dilanjutkan dengan pengenalan bilangan riil baik secara aksioma, ataupun melalui pembentukan dengan barisan Cauchy, ataupun potongan Dedekind pada bilangan rasional. Hasil yang mendasar kemudian dapat diperoleh, yang terpenting adalah sifat-sifat dari nilai mutlak seperti pertidaksamaan segitiga dan pertidaksamaan Bernoulli..

Bilangan riil atau bilangan real (dinotasikan ${\displaystyle \mathbb {R} }$ sebagai himpunan bilangan riil) merupakan bilangan yang mencakup bilangan irasional dan bilangan rasional. Bilangan riil dapat kita pandangi sebagai label dalam titik-titik di sepanjang garis horizontal sehingga angka-angkanya dapat mengukur jarak ke kiri dan ke kanan.^[4] Himpunan bilangan riil dapat dituliskan sebagai

${\displaystyle \mathbb {N} \subset \mathbb {Z} \subset \mathbb {Q} \subset \mathbb {R} }$.

• 
  Himpunan bilangan riil (${\displaystyle \mathbb {R} }$) terdiri dari bilangan asli (${\displaystyle \mathbb {N} }$), bilangan bulat (${\displaystyle \mathbb {Z} }$), dan bilangan rasional (${\displaystyle \mathbb {Q} }$).
• 
  Ilustrasi bilangan riil dengan titik-titik yang dilabeli angka-angka pada garis horizontal.^[5]

Limit merupakan konsep yang menjelaskan ketika suatu masukan atau indeks mendekati suatu nilai.^[6] Definisi maupun sifat-sifatnya dapat dibuktikan dengan menggunakan definisi limit (ε,δ).

Konsep kekonvergenan, sebagai dasar analisis, diperkenalkan melalui limit dan barisan. Beberapa kaidah yang mengatur proses pelimitan dapat diturunkan, dan beberapa limit dapat dihitung, serta deret takhingga, yang merupakan barisan yang khusus juga dipelajari. Deret pangkat digunakan untuk mendefinisikan dengan jelas beberapa fungsi yang penting, seperti fungsi eksponensial dan fungsi-fungsi trigonometri. Beberapa tipe penting dari subhimpunan bilangan riil, seperi himpunan-himpunan terbuka, himpunan-himpunan tertutup, himpunan-himpunan kompak, dan sifat-sifatnya dijelaskan kemudian.

Konsep mengenai kekontinuan dapat dijelaskan menggunakan limit. Penambahan, perkalian, komposisi, hasil kali dan haslil bagi dari fungsi-fungsi yang kontinu adalah fungsi yang kontinu juga, dan teorema nilai tengah yang penting juga terbukti.

Pada pencapaian ini, adalah sangat berguna untuk mempelajari ide dari kekontinuan dan kekonvergenan dengan lebih abstrak, agar kemudian dapat memperhitungkan ruang dari fungsi-fungsi. Ini dapat dilakukan dalam topologi himpunan titik dan menggunakan ruang metrik. Konsep-konsep seperti kekompakan, kelengkapan, ketersambungan, kekontinuan yang seragam, keterpisahan, peta Lipschitz, peta kontraktif, dapat didefinisikan dan diperiksa.

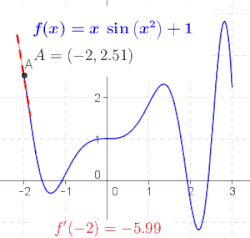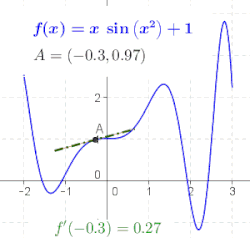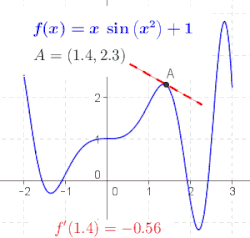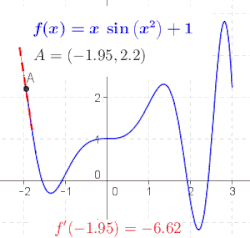
Turunan adalah konsep yang menjelaskan bagaimana perilaku fungsi berubah seiring perubahan nilai masukan. Ide mengenai turunan mungkin dapat diperkenalkan sebagai suatu proses pelimitan tertentu, dan hukum-hukum turunan yang umum dari kalkulus dapat dijelaskan dengan lebih terperinci.

Integral Riemann, dinamai dari Bernhard Riemann, merupakan integral yang didefinisikan dalam bentuk jumlah fungsi Riemann terhadap label dari suatu interval.

• Analisis kompleks
• Daftar topik analisis riil

1. ^ Tao, Terence (2003). "Lecture notes for MATH 131AH" (PDF). Course Website for MATH 131AH, Department of Mathematics, UCLA.
2. ^ Rudin, Walter (1976). Principles of Mathematical Analysis. Walter Rudin Student Series in Advanced Mathematics (Edisi 3rd). McGraw–Hill. ISBN 978-0-07-054235-8.
3. ^ Abbott, Stephen (2001). Understanding Analysis. Undergraduate Texts in Mathematics. New York: Springer-Verlag. ISBN 978-0-387-95060-0.
4. ^ Dale Varberg, Edward Purcell, Steve Rigdon (2006). Kalkulus Edisi Kesembilan, Jilid 1. hlm. 1. (Penerjemah: I Nyoman Susila, Ph. D, Penerbit Erlangga)
5. ^ Dale Varberg, Edward Purcell, Steve Rigdon (2006). Kalkulus Edisi Kesembilan. hlm. 2. (Penerjemah: I Nyoman Susila, Ph. D, Penerbit Erlangga)
6. ^ Stewart, James (2008). Calculus: Early Transcendentals (Edisi 6th). Brooks/Cole. ISBN 978-0-495-01166-8.