Diagram Euler

Artikel ini perlu diterjemahkan dari bahasa Inggris ke bahasa Indonesia. Artikel ini ditulis atau diterjemahkan secara buruk dari Wikipedia bahasa Inggris. Jika halaman ini ditujukan untuk komunitas bahasa Inggris, halaman itu harus dikontribusikan ke Wikipedia bahasa Inggris. Lihat daftar bahasa Wikipedia. Artikel yang sama sekali tidak diterjemahkan dapat dihapus secara cepat sesuai kriteria A2. Jika Anda ingin memeriksa artikel ini, Anda boleh menggunakan mesin penerjemah. Namun ingat, mohon tidak menyalin hasil terjemahan tersebut ke artikel, karena umumnya merupakan terjemahan berkualitas rendah.

Diagram Euler (/ˈɔɪlər/,) adalah diagram cara metik untuk mewakili himpunan dan hubungannya. Mereka sangat berguna untuk menjelaskan hierarki yang kompleks dan definisi yang tumpang tindih. Mereka mirip dengan teknik diagram himpunan lainnya, diagram Venn. Tidak seperti diagram Venn, yang menunjukkan semua kemungkinan hubungan antara set yang berbeda, diagram Euler hanya menampilkan relasi yang relevan.

Penggunaan pertama "lingkaran Eulerian" biasanya dikaitkan dengan ahli matematika Swiss Leonhard Euler (1707–1783). Di Amerika Serikat, diagram Venn dan Euler digabungkan sebagai bagian dari instruksi di teori himpunan sebagai bagian dari gerakan matematika baru tahun 1960-an. Sejak saat itu, mereka juga diadopsi oleh bidang kurikulum lain seperti membaca^[1] serta organisasi dan bisnis.

Diagram Euler terdiri dari bentuk tertutup sederhana dalam bidang dua dimensi yang masing-masing menggambarkan himpunan atau kategori. Bagaimana atau jika bentuk-bentuk ini tumpang tindih mendemonstrasikan hubungan antar set. Setiap kurva membagi bidang menjadi dua wilayah atau "zona": interior, yang secara simbolis mewakili elemen dari himpunan, dan eksterior, yang mewakili semua elemen yang bukan anggota himpunan. Kurva yang tidak tumpang tindih mewakili set terputus-putus, yang tidak memiliki elemen yang sama. Dua kurva yang tumpang tindih mewakili himpunan yang berpotongan, yang memiliki elemen yang sama; zona di dalam kedua kurva mewakili himpunan elemen yang sama untuk kedua himpunan (perpotongan dari himpunan). Sebuah kurva yang seluruhnya berada di dalam interior lainnya adalah subhimpunan darinya.

Diagram Venn adalah bentuk diagram Euler yang lebih terbatas. Diagram Venn harus berisi semua 2ⁿ secara logis kemungkinan zona tumpang tindih antara kurva n , mewakili semua kombinasi penyertaan/pengecualian himpunan konstituennya. Region bukan bagian dari himpunan ditunjukkan dengan mewarnai mereka dengan warna hitam, berbeda dengan diagram Euler, di mana keanggotaan dalam himpunan ditunjukkan dengan tumpang tindih serta warna.

Artikel ini sedang dalam perbaikan. CATATAN: bagian ini jangan dihapus. Untuk menghindari konflik penyuntingan, mohon jangan melakukan penyuntingan selama pesan ini ditampilkan. Halaman ini terakhir disunting oleh Taylorbot (Kontrib • Log) 195 hari 433 menit lalu.

Seperti yang ditunjukkan pada ilustrasi di sebelah kanan, Sir William Hamilton dalam bukunya yang diterbitkan secara anumerta Lectures on Metaphysics and Logic (1858–60) secara keliru menegaskan ... abstraksi Logika "(hlm. 180) bukanlah Leonhard Paul Euler (1707–1783) melainkan Christian Weise (1642–1708) dalam bukunya Nucleus Logicae Weisianae yang muncul pada 1712 secara anumerta, bagaimanapun, buku terakhir sebenarnya ditulis oleh Johann Christian Lange daripada Weise.^[2][3] He references Euler's Letters to a German Princess [Partie II, Lettre XXXV, February 17, 1791, ed. Cournot (1842), pp. 412-417. – ED.]^{[nb 1]}

Dalam ilustrasi Hamilton, empat proposisi kategorikal yang dapat terjadi dalam silogisme seperti yang disimbolkan oleh gambar A, E, I dan O adalah:^[4]

• J: The Universal Affirmative , Contoh: "Semua logam adalah unsur".
• E: The Universal Negative , Contoh: "Tidak ada logam yang merupakan zat majemuk".
• I: The Particular Affirmative , Contoh: "Beberapa logam rapuh".
• O: The Particular Negative , Contoh: "Beberapa logam tidak rapuh".

Dalam karyanya tahun 1881 Symbolic Logic Bab V "Diagrammatic Representation", John Venn (1834–1923) mengomentari prevalensi yang luar biasa dari diagram Euler:

"...dari enam puluh risalah logis pertama, yang diterbitkan selama sekitar abad terakhir, yang dikonsultasikan untuk tujuan ini: -beberapa secara acak, karena kebetulan mereka paling mudah diakses: -tampaknya tiga puluh empat meminta bantuan diagram, hampir semua ini memanfaatkan Skema Eulerian. "(Catatan kaki 1 halaman 100)

Namun demikian, ia berpendapat, "ketidakmampuan skema ini untuk tujuan Logika yang sangat umum" (halaman 100), "Ini cocok tetapi buruk bahkan dengan empat proposisi dari Logika umum yang biasanya diterapkan." Venn mengakhiri babnya dengan observasi yang diilustrasikan dalam contoh di bawah — bahwa penggunaannya didasarkan pada praktik dan intuisi, bukan pada praktik algoritme yang ketat:

“Nyatanya ... diagram-diagram tersebut tidak hanya tidak cocok dengan skema proposisi biasa yang digunakan untuk menggambarkannya, tetapi tampaknya tidak memiliki skema proposisi yang diakui sehingga mereka dapat secara konsisten berafiliasi. " (hlm. 124–125)

- Proses pengembangan -

• 
  Diagram Venn menunjukkan semua kemungkinan persimpangan.
• 
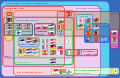
  Diagram Euler memvisualisasikan situasi nyata, hubungan antara berbagai organisasi supranasional Eropa. (versi yang dapat diklik)
• 
  Diagram lucu membandingkan Euler dan diagram Venn.
• 
  Diagram euler dari jenis segitiga, menggunakan definisi bahwa segitiga sama kaki memiliki setidaknya (bukan persis) 2 sisi yang sama.
• 
  Diagram Euler dari terminologi Kepulauan Inggris.
• 
  22 (dari 256) diagram Venn yang pada dasarnya berbeda dengan 3 lingkaran (atas) dan diagram Euler yang sesuai (bawah)
  Beberapa diagram Euler tidak tipikal, dan beberapa bahkan setara dengan diagram Venn. Area diarsir untuk menunjukkan bahwa mereka tidak mengandung elemen.

• Diagram Spider - perpanjangan dari diagram Euler yang menambahkan keberadaan ke persimpangan kontur.

Menurut tanggal penerbitan:

• Sir William Hamilton 1860 Lectures on Metaphysics and Logic edited by Henry Longueville Mansel and John Veitch, William Blackwood and Sons, Edinburgh and London.
• W. Stanley Jevons 1880 Elementary Lessons in Logic: Deductive and Inductive. With Copious Questions and Examples, and a Vocabulary of Logical Terms, M. A. MacMillan and Co., London and New York.
• Alfred North Whitehead and Bertrand Russell 1913 1st edition, 1927 2nd edition Principia Mathematica to *56 Cambridge At The University Press (1962 edition), UK, no ISBN.
• Louis Couturat 1914 The Algebra of Logic: Authorized English Translation by Lydia Gillingham Robinson with a Preface by Philip E. B. Jourdain, The Open Court Publishing Company, Chicago and London.
• Emil Post 1921 "Introduction to a general theory of elementary propositions" reprinted with commentary by Jean van Heijenoort in Jean van Heijenoort, editor 1967 From Frege to Gödel: A Source Book of Mathematical Logic, 1879–1931, Harvard University Press, Cambridge, MA, ISBN 0-674-32449-8 (pbk.)
• Claude E. Shannon 1938 "A Symbolic Analysis of Relay and Switching Circuits", Transactions American Institute of Electrical Engineers vol 57, pp. 471–495. Derived from Claude Elwood Shannon: Collected Papers edited by N.J.A. Solane and Aaron D. Wyner, IEEE Press, New York.
• Hans Reichenbach 1947 Elements of Symbolic Logic republished 1980 by Dover Publications, Inc., NY, ISBN 0-486-24004-5.
• Veitch, Edward Westbrook (1952-05-03) [1952-05-02]. "A Chart Method for Simplifying Truth Functions". Transactions of the 1952 ACM Annual Meeting. ACM Annual Conference/Annual Meeting: Proceedings of the 1952 ACM Annual Meeting (Pittsburgh, Pennsylvania, USA). New York, USA: Association for Computing Machinery (ACM): 127–133. doi:10.1145/609784.609801.
• Karnaugh, Maurice (November 1953) [1953-04-23, 1953-03-17]. "The Map Method for Synthesis of Combinational Logic Circuits" (PDF). Transactions of the American Institute of Electrical Engineers, Part I: Communication and Electronics. 72 (5): 593–599. doi:10.1109/TCE.1953.6371932. Paper 53-217. Diarsipkan dari asli (PDF) tanggal 2017-04-16. Diakses tanggal 2017-04-16.
• Frederich J. Hill and Gerald R. Peterson 1968, 1974 Introduction to Switching Theory and Logical Design, John Wiley & Sons, NY, ISBN 978-0-471-39882-0.
• Sandifer, Ed (January 2004). "How Euler Did It" (PDF). maa.org. Diarsipkan dari asli (PDF) tanggal 2013-01-26.

Wikimedia Commons memiliki media mengenai Euler diagrams.

• Euler Diagrams. Brighton, UK (2004).What are Euler Diagrams?